Efficient uncertainty quantification for Monte Carlo dose calculations using importance (re-)weighting - PDF Version
Pia Stammer, Lucas Burigo, Oliver Jäkel, Martin Frank, Niklas Wahl
Physics in Medicine and Biology 2021 October; 66: 22 doi:10.1088/1361-6560/ac287f.
What was your motivation for initiating this study?
The analysis and mitigation of uncertainties is an essential topic during work in critical applications such as radiation therapy. For a similar reason, accurate Monte Carlo (MC) methods are frequently used for dose calculations in radiotherapy treatment planning. However, their long computation times impede the performance of comprehensive uncertainty analyses, which would require additional computational effort.
We work within the interdisciplinary graduate school the Helmholtz Information and Data Science School for Health (HIDSS4Health), which was set up by several German institutions to improve use of data science in medical fields. We profit both from the domain knowledge provided by the German Cancer Research Center and the methodological knowledge that has been developed in the research group for computational science and mathematical methods at Karlsruhe Institute of Technology. Our aim in this study was to bring mathematical methods that are used in statistics and uncertainty quantification (UQ) into application in order to find and implement a more efficient approach to UQ in MC dose computations.
The large set of particle trajectories in MC dose calculations usually covers the total relevant area of both the physical and parameter space. When different error scenarios are computed, therefore, many of the simulated particles in one case are also relevant for the other. This gave us the idea that we could find a way to re-use computed particle trajectories. The formulation of the initial phase space of particles, i.e., their position, energy and momentum, as a probability distribution then helped us to draw a connection to a well-known method from statistics: importance sampling. Here, the expected value of a function for a variable with distribution f is computed through use of samples from a different distribution g. Applied to our problem, we saw the potential to formulate an error scenario as a change in the probability distributions that describe the phase space. It would then be possible to use the sample of particle trajectories from one computation to estimate the dose for many different scenarios.
What were the main challenges during the work?
Using the multivariate Gaussian input model, the mathematical formulation of the approach for a single beam and set-up uncertainties was relatively straightforward. The three main challenges that followed are listed here.
- We had to adapt the model to work for an intensity modulated particle therapy (IMPT) framework with a large number of pencil beams and choose appropriate distributions to model the intended error as well as compute the set of particle histories to be used for all scenario reconstructions.
- We had to implement the approach within pre-existing code frameworks for patient computations. We used the treatment planning software matRad to generate radiation plans and the MC engine TOPAS to compute the required particle histories. It was necessary to write extensions to TOPAS, which imported the correct plan, set up the beam configuration corresponding to the chosen input distribution and then stored the computed particle histories to later reconstruct the dose for different error scenarios. Here, for example, inconsistencies between the coordinate systems of different software packages had to be taken into account.
- We had to incorporate range errors, which, unlike set-up errors, affect a previously deterministic parameter of the simulation ‑ namely the tissue density. Our approach depends on the existence of a probability distribution of parameters that are affected by the error. If there is no such set of parameters, all histories that are used for the reconstruction are computed through use of the single deterministic value and there is no statistical information on what happens if this parameter takes on a different value. We were able to work around this issue for range errors by approximating changes in the patient density according to the associated changes in the particle range and then by using the Bragg-Kleemann rule to translate these uncertainties in the range to uncertainties in the particle energy. Since the particle energy usually has a non-trivial probability distribution, the regular framework could again be applied.
What is the most important finding of your study?
Uncertainty estimates, such as expected dose value and variance for set-up errors in MC dose calculations, can be efficiently computed from a single set of particle histories, with high agreements of 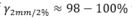 to standard scenario estimates.
to standard scenario estimates.
.jpg.aspx)
Also, it is possible to approximate range errors that are caused by conversion into WEPL by using only the parameters of the energy distribution of the initial primary particles. In this case, some artefacts and systematic deviations occur in the solution for the dose variance; however, the expected dose value also exhibits high agreement to the reference solutions.
Further, the multivariate input distribution enables the computation of uncertainty estimates in principle for arbitrary correlation models with respect to the errors in each pencil beam. Therefore, complex correlation patterns that would usually require a vast number of scenario computations and elaborate computational set-up can be considered easily and results for several uncertainty models can be reconstructed from the same set of simulated histories.
What are the implications of this research?
This approach enables the accurate quantification of uncertainty with MC dose calculation while it requires minimal intrusion into the used algorithm. It enables direct or retrospective scoring of multiple error scenarios and corresponding uncertainty metrics in just one MC simulation. At the same time, it facilitates the use of flexible, complex uncertainty models, and therefore its use encourages us to rethink the way in which uncertainties in space and time can be modelled beyond worst-case scenario approaches. Therefore, our research is a step towards the reconciliation of efficient UQ with MC dose calculation, which could translate into robust optimisation and more realistic uncertainty models.

Pia Stammer
Karlsruhe Institute of Technology,
Steinbuch Centre for Computing,
Karlsruhe, Germany and
German Cancer Research Center — DKFZ,
Department of Medical Physics in Radiation Oncology,
Heidelberg, Germany and
Helmholtz Information and Data Science School for Health,
Karlsruhe/Heidelberg, Germany
pia.stammer@kit.edu